Or, le soleil, se levant sur un horizon pur, annonçait une journée magnifique, une de ces belles journées d’automne qui sont comme les derniers adieux de la saison chaude.

Il s’agissait donc de compléter les éléments des observations de la veille, en mesurant la hauteur du plateau de Grande-Vue au-dessus du niveau de la mer.

« Ne vous faut-il pas un instrument analogue à celui qui vous a servi hier ? demanda Harbert à l’ingénieur.

– Non, mon enfant, répondit celui-ci, nous allons procéder autrement, et d’une manière à peu près aussi précise. »

Harbert, aimant à s’instruire de toutes choses, suivit l’ingénieur, qui s’écarta du pied de la muraille de granit, en descendant jusqu’au bord de la grève. Pendant ce temps, Pencroff, Nab et le reporter s’occupaient de divers travaux.

Cyrus Smith s’était muni d’une sorte de perche droite, longue d’une douzaine de

pieds, qu’il avait mesuré aussi exactement que possible, en la comparant à sa propre taille, dont il connaissait la hauteur à une ligne près. Harbert portait un fil à plomb que lui avait remis Cyrus Smith, c’est-à-dire une simple pierre fixée au bout d’un fibre flexible.

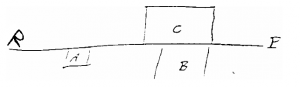
Arrivé à une vingtaine de pieds de la lisière de la grève, et à cinq cents pieds environ de la muraille de granit, qui se dressait perpendiculairement, Cyrus Smith enfonça la perche de deux pieds dans le sable, et, en la calant avec soin, il parvint, au moyen du fil à plomb, à la dresser perpendiculairement au plan de l’horizon.

Cela fait, il se recula de la distance nécessaire pour que, étant couché sur le sable, le rayon visuel, parti de son oeil, effleurât à la fois et l’extrémité de la perche et la crête de la muraille. Puis il marqua soigneusement ce point avec un piquet.

Alors, s’adressant à Harbert :

« Tu connais les premiers principes de la géométrie ? lui demanda-t-il.

– Un peu, monsieur Cyrus, répondit Harbert, qui ne voulait pas trop s’avancer.

– Tu te rappelles bien quelles sont les propriétés des triangles semblables ?

– Oui, répondit Harbert. Leurs côtés homologues sont proportionnels.

– Eh bien, mon enfant, je viens de construire deux triangles semblables, tous deux rectangles : le premier, le plus petit, a pour côtés la perche perpendiculaire, la distance qui sépare le piquet du bas de la perche, et mon rayon visuel pour hypoténuse ; le second a pour côtés la muraille perpendiculaire, dont il s’agit de mesurer la hauteur, la distance qui sépare le piquet du bas de cette muraille, et mon rayon visuel formant également son hypoténuse, – qui se trouve être la prolongation de celle du premier triangle.

– Ah ! monsieur Cyrus, j’ai compris ! s’écria Harbert. De même que la distance du piquet à la perche est proportionnelle à la distance du piquet à la base de la muraille, de même la hauteur de la perche est proportionnelle à la hauteur de cette muraille.

– C’est cela même, Harbert, répondit l’ingénieur, et quand nous aurons mesuré les deux premières distances, connaissant la hauteur de la perche, nous n’aurons plus qu’un calcul de proportion à faire, ce qui nous donnera la hauteur de la muraille et nous évitera la peine de la mesurer directement. »

Les deux distances horizontales furent relevées, au moyen même de la perche, dont la longueur au-dessus du sable était exactement de dix pieds.

La première distance était de quinze pieds entre le piquet et le point où la perche était enfoncée dans le sable.

La deuxième distance, entre le piquet et la base de la muraille, était de cinq cents pieds.

Ces mesures terminées, Cyrus Smith et le jeune garçon revinrent au Cheminées.

Là, l’ingénieur prit une pierre plate qu’il avait rapportée de ses précédentes expéditions, sorte de schiste ardoisier, sur lequel il était facile de tracer des chiffres au moyen d’une coquille aiguë. Il établit donc la proportion suivante :

15 : 500 :: 10 : x

500 × 10 = 5 000

5 000

15

= 333,33

D’où il fut établi que la muraille de granit mesurait trois cent trente-trois pieds

de hauteur ¹.

(1) Il s’agit du pied anglais, qui vaut 30 centimètres.

Commentaires :

Après avoir un schéma et rédigé la démonstration de Jules Verne tu pourras calculer la hauteur, en mètre, de la muraille.

O mathématiques sévères, je ne vous ai pas oubliées, depuis que vos savantes

leçons, plus douces que le miel, filtrèrent dans mon cœur, comme une onde

rafraîchissante.

…

A l’aide de votre lait fortifiant, mon intelligence s’est rapidement développée, et

a pris des proportions immenses, au milieu de cette clarté ravissante dont vous

faites présent, avec prodigalité, à ceux qui vous aiment d’un sincère amour.

Arithmétique ! algèbre ! géométrie ! trinité grandiose ! triangle lumineux ! Celui

qui ne vous a pas connues est un insensé.

…

Vous, ô mathématiques concises, par l’enchaînement rigoureux de vos

propositions tenaces et la constance de vos lois de fer, vous faites luire, aux yeux

éblouis, un reflet puissant de cette vérité suprême dont on remarque l’empreinte

dans l’ordre de l’univers. Mais, l’ordre qui vous entoure, représenté surtout par la

régularité parfaite du carré, l’ami de Pythagore, est encore plus grand.

…

Vous me donnâtes la prudence opiniâtre qu’on déchiffre à chaque pas dans vos

méthodes admirables de l’analyse, de la synthèse et de la déduction. (…) Vous me

donnâtes la logique, qui est comme l’âme elle-même de vos enseignements, pleins

de sagesse, mon intelligence sentit s’accroître du double ses forces audacieuses.

Rien ne sert de courir, il faut partir à point.

Le lièvre et la tortue en sont un témoignage.

« Gageons, dit celle-ci, que vous n’atteindrez point

Sitôt que moi ce but. – Sitôt ? êtes-vous sage ?

Repartit l’animal léger.

Ma commère, il vous faut purger

Avec quatre grains d’ellébore.

– Sage ou non, je parie encore. »

Ainsi fut fait, et de tous deux

On mit près du but les enjeux.

Savoir quoi, ce n’est pas l’affaire,

Ni de quel juge l’on convint.

Notre lièvre n’avait que quatre pas à faire :

J’entends de ceux qu’il fait, lorsque, prêt d’être atteint,

Il s’éloigne des chiens, les renvoie aux calendes

Et leur fait arpenter les landes.

Ayant, dis-je, du temps de reste pour brouter,

Pour dormir et pour écouter

D’où vient le vent, il laisse la tortue

Aller son train de sénateur.

Elle part, elle s’évertue ;

Elle se hâte avec lenteur.

Lui cependant méprise une telle victoire,

Tient la gageure à peu de gloire,

Croit qu’il y va de son honneur

De partir tard. Il broute, il se repose,

Il s’amuse à tout autre chose

Qu’à la gageure. A la fin, quand il vit

Que l’autre touchait presque au bout de la carrière,

Il partit comme un trait; mais les élans qu’il fit

Furent vains : la tortue arriva la première.

« Eh bien ! lui cria-t-elle, avais-je pas raison ?

De quoi vous sert votre vitesse ?

Moi, l’emporter ! et que serait-ce

Si vous portiez une maison? »

Commentaires :

La tortue part immédiatement au moment du départ puis à « un train de sénateur » marche à une vitesse régulière et parcourt la distance totale en un certain temps. A la moitié de ce temps, elle a parcouru la moitié de la distance totale. Au trois quarts de ce temps, elle a parcouru les trois quarts de la distance totale. Sa vitesse étant constante, la distance qu’elle parcourt est proportionnelle au temps écoulé. Le parcours de la tortue peut se résumer par la formule D = V × T ( V est le coefficient de proportionnalité entre le temps T et la distance D ). Cette formule se traduit graphiquement par une droite.

Pour le lièvre il en va tout autrement. Au début « il broute, il se repose », le temps passe et la distance parcourue est presque nulle. Au trois quarts du temps, il n’a pas parcouru les trois quarts de la distance totale, loin s’en faut. Tout à la fin « il partit comme un trait », en peu de temps il a parcouru une grande distance.

On peut représenter les deux parcours ainsi :

Mais quand la tortue arrive, le lièvre n’a pas encore parcouru toute la distance. Mais quand la tortue arrive, le lièvre n’a pas encore parcouru toute la distance…

Le Client

Garçon, l’addition !

Le Garçon

Voilà. (Il sort son crayon et note.) Vous avez… deux oeufs durs, un veau, un petit pois, une asperge, un fromage avec beurre, une amande verte, un café filtre, un téléphone.

Le Client

Et puis des cigarettes !

Le Garçon

(Il commence à compter)

C’est ça même… des cigarettes… … Alors ça fait…

Le Client

N’insistez pas, mon ami, c’est inutile, vous ne réussirez jamais.

Le Garçon

!!!

Le Client

On ne vous a donc pas appris à l’école que c’est ma-thé-ma-tique-ment impossible d’additionner des choses d’espèces différentes !

Le Garçon

!!!

Le Client

(élevant la voix)

Enfin, tout de même, de qui se moque-t-on ?… Il faut réellement être insensé pour oser essayer de tenter d’ « additionner » un veau avec des cigarettes, des cigarettes avec un café filtre, un café filtre avec des amandes vertes et des oeufs durs avec des petits pois, des petits pois avec un téléphone… Pourquoi pas un petit pois avec un grand officier de la Légion d’Honneur, pendant que vous y êtes ! (Il se lève)

Non, mon ami, croyez-moi, n’insistez pas, ne vous fatiguez pas, ça ne donnerait rien… pas même le pourboire !

(Et il sort en emportant le rond de serviette à titre gracieux.)

Mon enthousiasme pour les mathématiques avait peut-être eu pour base principale mon horreur pour l’hypocrisie.

Suivant moi l’hypocrisie était impossible en mathématiques et, dans ma simplicité juvénile, je pensais qu’il en était ainsi dans toutes les sciences où j’avais ouï qu’elles s’appliquaient. Que devins-je quand je m’aperçus que personne ne pouvait m’expliquer comment il se faisait que moins par moins donne plus ( – × – = + ) ? (C’est une des bases fondamentales de la science qu’on appelle algèbre).

On faisait bien pis que de ne pas m’expliquer cette difficulté (qui sans doute est explicable car elle conduit à la vérité), on me l’expliquait par des raisons évidemment peu claires pour ceux qui me les présentaient.

Monsieur Chabert pressé par moi s’embarrassait, répétait sa leçon, celle précisément contre laquelle je faisais des objections, et finissait par avoir l’air de me dire :

« Mais c’est l’usage, tout le monde admet cette explication. Euler et Lagrange, qui apparemment valaient autant que vous, l’ont bien admise. Nous savons que vous avez rempoté un premier prix de belles-lettres. »

Je fus longtemps à me convaincre que mon objection sur – × – = + ne pouvait absolument pas entrer dans la tête de M. Chabert, que M. Dupuy n’y répondrait jamais que par un sourire de hauteur, et que les forts auxquels je faisais des questions se moqueraient toujours de moi.

J’en fus réduit à ce que je me dis encore aujourd’hui : il faut bien que – par – donne + soit vrai, puisque évidemment, en employant à chaque instant cette règle dans le calcul, on arrive à des résultats vrais et indubitables.

Mon grand malheur était cette figure :

Supposons que RP soit la ligne qui sépare le positif du négatif, tout ce qui est au-dessus est positif, comme négatif tout ce qui est dessous ; comment en prenant le carré B autant de fois qu’il y a d’unités dans le carré A, puis-je parvenir à faire changer de côté au carré C ?

Et, en suivant une comparaison gauche que l’accent souverainement trainard et grenoblois de M. Chabert rendait encore plus gauche, supposons que les quantités négatives sont les dettes d’un homme, comment en multipliant 10.000 francs de dette par 500 francs, cet homme aura-t-il ou parviendra-t-il à avoir une fortune de 5.000.000, cinq millions ?

– × – = + m’avait donné beaucoup de chagrin.

Commentaire :

Pour que celui-ci surmonte son chagrin, qu’est ce que son professeur de mathématiques aurait du dire à Henri ?